Technical

Using Celery+Python to make a Distributed Genetic Algorithm

Note: If you like to follow along with complete source, feel free to grab this project on github.

Celery is a distributed task queue that integrates smoothly with python. I stumbled upon it and immediately saw it as a cool technology looking for an application. You can define tasks in python by just adding a decorator (@task) that can be performed in the background asynchronously by hungry worker compute nodes. For example, here is a sample (simple) task gratuitously lifted from the basic celery tutorial:

@task
def add(x, y):
    return x + y

You can then call the task with its “delay” method and it will be serialized, whisked away to Celery’s backend queue, unserialized by a worker, computed, and then the result will be ferried back to the python caller:

>>> from tasks import add
>>> add.delay(4, 4)
>>> result.get()
8

What is especially nice about this is how seamless it is. If your prior exposure to parallelization is something like MPI in C++, the simplicity and elegance of celery is refreshing. It just works, and for expensive parallel tasks it is a nice way of circumventing the GIL in python.

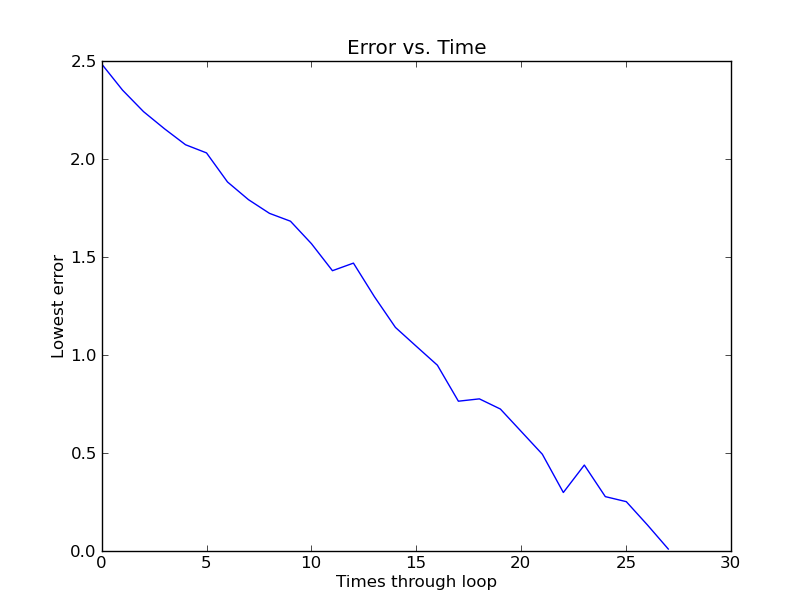
My PhD research often involves genetic algorithms. The idea is that you have an array of artificial genomes (which are themselves often lists of numbers) and a way of judging these genomes (an error function of some kind). Iteratively you apply the error function to weed out the worst of these artificial genomes, and replace those worst genomes with slight variations of the better ones. The hope is that over time you can find a genome that minimizes the error function (usually called the fitness function in GA parlance).

Usually the performance bottleneck in GAs is evaluating each genome through the fitness function. For example, sometimes this evaluation can consist of expensive physics simulations (e.g. simulations of virtual creatures).

What is nice from a parallelization standpoint, is that each simulation is done on a per-genome basis and is (usually) independent of every other genome. So if you had a population of 1000 genomes that you need to evaluate, you can create a celery task for each of them that can be offloaded to either spare cores on the same computer or onto worker instances on other computers.

Of course, celery will be handy not only for GAs but wherever you have many expensive tasks that are independent of each other. For example, rendering individual frames of a ray-tracing animation or multiplying many large matrices. If you can decompose your computational bottleneck into significant independent chunks, Celery may be a good fit for easily reaping the benefits of parallelization.

For the genetic algorithm application, I just had to wrap the fitness function as a celery task:

@task
def evaltask(domain,genome):
 fit=domain.evaluate(genome)
 return fit

And then I augmented the serial evaluation of the genomes (shown here):

#evaluate sequential
 if(not eval_concurrent):
  for k in population:
   k.fitness = dom.evaluate(k)

With the parallel evaluation that uses the celery server:

#else evaluate concurrently
else:
  tasks=[]
  for ind in population:
   tasks.append(evaltask.subtask((dom,ind)))

  job = TaskSet(tasks=tasks)

  result=job.apply_async()
  fits=result.join()

What this code does is make a list of celery subtasks, one for each genome to be evaluated. It composes this into a larger “taskset,” which is run asychronously, and the results are gathered (in order) by the join call once they all complete. If each task is non-trivial (i.e. it takes significantly longer to run than the overhead associated with serializing it and throwing it to celery), then the speed-up gained from paralellization can be very nice.

Feel free to check out the complete source on github (including the celeryconfig.py file that).

Using concurrency requires a working celery install (see http://www.celeryproject.org/tutorials/first-steps-with-celery/ for how to run celery, it is fairly simple to install):

You can install Celery either via the Python Package Index (PyPI) or from source.

To install using pip:

1
$ pip installCelery

To install using easy_install,:

1
$ easy_install Celery

And a backend for celery is necessary for it to run. The default is rabbitMQ, available on ubuntu as package: rabbitmq-server

Frankenstein Meets Darwin

Teaser video:



“Neuroevolution,” which literally means “Evolving brains,” sounds like a tired sci-fi plot: Scientists create a super-smart computer that gets out of control and goes on a wild rampage, stopped only seconds from starting a nuclear holocaust (or not, in the case of the Terminator movies).

Yet, far from fiction, neuroevolution is what I do on a daily basis: Evolving artificial brains in a computer is the foundation of my Ph.D. research. It’s not something I came up with, and is not a brand new idea — neuroevolution is an approach to artificial intelligence that has been around for 15 years. It’s inspired by how biological brains evolved through natural evolution.

“Oh, um. You evolve…brains? In a computer?”

Whenever you meet someone new, the question, “What do you do?” inevitably percolates into conversation. To avoid the glazed-over eyes that tend to result from my explanations,  my vague canned response is that I am a graduate student in computer science. Although what I do is not insanely complicated, it is far-enough removed from typical day-to-day experience that explaining it in a sound-bite is damn near impossible.

The more abstract a concept is, the craftier one must be to describe it both intelligably and succinctly. For example, it’s fairly easy to explain what Sushi is to someone who doesn’t know because Sushi is “concrete” — it’s touchable, edible and related to “fish,” a universal concept.

You could say, “carefully-prepared raw fish,” and not be too far off the mark. But it is harder to explain to the uninitiated what electric current is, because it is not something “physical” nor directly visible. But although electric current is abstract, we can quickly begin to understand it by relating it to something familiar and “real” like a river current. Electricity “flows” in a similar way to water.

So, while someone’s eyes might glaze over when you talk about electrons, relating electricity to a river is more intuitive. So it turns out that only I am to blame for the glazed-over eyes of my acquaintances because I have not been clever enough to explain clearly and simply what I do. And so I hope to atone for past blank stares of nonrecognition with this post: Neuroevolution is simple and interesting, and I want to tell you why in an easy way.

Dancing Bees

Have you ever been to a zoo? Or an aquarium? The seemingly limitless variety of living creatures, and the amazing things they can do, is fascinating. An archer fish shoots a powerful, carefully-aimed stream of water from its mouth to knock insects into the water, then quickly swallows the stunned critters. A bumblebee dances in two separate ways, depending on how far away it is from food, to show its comrades where to forage. Crows fashion tools and even learn to bait-fish with bread crumbs. The diversity and complexity of nature is awe-inspring.

The source of this diversity and complexity is natural evolution. Although it is hard at first to accept that an unguided process could produce such magnificent artifacts (like your face,  you handsome reader), evolution is nearly universally accepted by scientists because of an overwhelming amount of evidence, such as fossils and vestigial organs.

“Nothing in Biology makes sense except in the light of evolution,” said a famous evolutionary Biologist, Theodosious Dobzhansky. If you believe in evolution, then you also must believe that evolution shaped our brains; our impressive intelligence is somehow the result of billions of years of trial and error experiments.

The point is that, without intelligence, evolution created a ton of really cool things, including our own intelligence. This mind-blowing possibility hints at the potential of neuroevolution: Perhaps we can harness the general process of evolution within a computer to evolve intelligent computer-brains! Trippy, right? But, before we are ready for a more complete description, I want to briefly digress and talk about artificial intelligence in general, the field of research that seeks to make smarter machines.

And what country is Toronto in, Watson?

Perhaps most of us are most familiar with Artificial Intelligence from movies such as 2001: A Space Oddessey, AI, Stealth, the Terminator, etc. In these movies scientists create an intelligent computer, and then it goes crazy and kills everybody. One part of this is based in reality: There are researchers that try to create more intelligent computers. In fact, I am one of those researchers.

To put your minds at rest, current research in AI is far from creating true human level intelligence. I’d guess that it will at least be a few decades yet before we reach that ambitious goal. A question people often ask is “Why?”: Why would we want intelligent computer programs? There are many different answers. One might side-step the “why” and appeal to curiosity; I for one, am curious about what intelligence is, and how we can better understand it. I think we might truly understand intelligence only when we can recreate it.

But there are also practical reasons we might want intelligent programs, too. For example, it wouldn’t be practical for Amazon to hire a massive team to create a personalized list of products one might like to buy for everyone who ever purchased things on Amazon. However, with AI techniques, a computer can find correlations like: people who bought product X also tended to buy product Y, and from these correlations automatically make personalized lists. More and more tasks that once had to be done painfully by hand, like arithmetic or checking spelling, can now be automated by computer programs with a small spark of what might be called intelligence.

There have been many interesting successes of AI. I’ll highlight two of the most famous here.

The first is when the best chess player in the world, Gary Kasparov, lost to Deep Blue, a supercomputer made by IBM. We once thought that chess was something that required true intelligence to master, because the game is deep, has many complicated strategies, and is difficult for humans to master. However, it is clear that chess does not require true intelligence to master, because deep blue, although it is very good at chess, can not do anything else at all. It won only by considering many many moves, using brute force calculation impossible for humans.

A second very famous success of AI is Watson, the Jeopardy-playing AI. It beat Ken Jennings, arguably the best jeopardy player of all time. This at first seems incredibly impressive, and it is! Who would think that a computer could be competitive with humans in a task like general question and answer? It is especially impressive because the questions in jeopardy tend to be playful and tricky.

However, Watson, like Deep Blue, is far from any “true AI” in that it is not “creative.” It won by clever human-designed algorithms coupled with four terabytes of human-curated data (Wikipedia and more). Also informative was its embarassing failure to recognize that “Toronto” is not a US city. Watson, like Deep Blue, does not have ‘general intelligence’ — it can only answer questions, and does not ‘reason’ in the traditional sense but again relies on cleverly designed tricks, raw brute force, and an enormous database of curated facts to perform well. Wouldn’t you be pretty good at jeopardy too if you could browse all of Wikipedia in a fraction of a second?

These Watson and Deep Blue approaches, although impressive and practical, seem to have almost no relation to general intelligence, which is what I am curious about. Why is that a toddler can still do things that a supercomputer can’t?

We only have one working example of general intelligence: Humans. And humans are the result of natural evolution; so, in order to create artificial intelligence, isn’t the most obvious approach to follow that one working example and examine evolving brains through artificial evolution? Of course, it’s not the only approach, but it has precedent on its side.

Evolution: Natural and Artificial

Before explaining the strange concept of artificial evolution within a computer, it’d be good to first understand how natural evolution works. How does it create organisms that are well-adapted to their environments like archer fishes or bumblebees? While we might all remember some vague ideas from science class involving “survival of the fittest” and “natural selection,”here are the three simple, concrete principles that underlie evolution:

1) Selection
In nature, animals typically have more children than can survive in the world. There’s not enough food for all the rabbits, and in addition wolves will eat those that are too slow. Natural selection is just that a lot of animals die before they reproduce. It is like a filter that generally only allows better-adapted animals to pass through.

Animals better at surviving and reproducing will tend to have more offspring, which spreads their genes and physical traits onwards. Animals worse at surviving and reproducing have less chance of spreading their genes. So, a gene that makes a rabbit faster might spread, while a gene that makes a rabbit slower would probably die out, because wolves might catch most slow rabbits before they had a chance to make rabbit babies.

While in nature animals are ‘selected’ naturally if they survive long enough to reproduce, selection can also be artificial. That is, humans can do the selecting instead of nature: Plant breeders might choose to mate the prettiest flowers together, or dog breeders might choose dogs that are smaller or friendlier or cuter, hoping that the children of that dog will also share those traits. We breed race horses for speed, breed cows to give more milk, and so on.

Selection, whether artificial or natural, tends to give evolution some direction, whether towards cuter dogs or faster rabbits better able to evade wolves.

2) Variation
The first principle was selection, that some animals would spread their genes, and others wouldn’t, and that evolution is given some sort of direction by what we select for. Nature selects for the ability to survive and reproduce, but human breeders may select dogs for cuteness instead.

The second principle is variation. That is, every dog is not exactly the same; dogs vary. Some racehorses might run faster or slower, some flowers might be prettier or uglier, and some archer fish might be more or less accurate at drilling insects with its built-in squirt gun. Variation enables selection to push evolution in some particular direction.

If all dogs were exactly the same (no variation), selection would have no distinctions to make among those dogs; you would find no cuter dogs because they would all be of the same cuteness.

Variation in itself doesn’t provide a direction, because it may create uglier dogs more often than it creates cuter dogs. But, selection among a variation on animals can push evolution in a direction, because it might filter out those uncute dogs; a human breeder would breed together the cute ones and not the uncute ones. What variation does is give that breeder choices.

3) Heritability
The third principle is heritability. Evolution requires that variation is generally passed on to its children.
People might say you resemble your mother, or that you have your father’s eyes: You resemble your parents. The reason for this is that your DNA, all of your genes, is a combination of your parents’ genes.

Heritability is the property that a child resembles their parent. If this wasn’t the case then there would be no continuity — if a bumblebee gave birth to a chipmunk, then all would be chaos. In that crazy world, you would never be able to find a really cool bumblebee if that is what you were were looking for, because a bumblebee’s children could be anything.

Another way of looking at this is by thinking about the game “telephone.” There is a line of kids, and the first kid thinks of a clever phrase. He then whispers it to the second kid, who whispers it to the third, and so on. By the end, the message is horribly garbled. In this situation there is little heritability, because the message has changed so much.

On the other hand, if one simply forwards an email without making any changes, the message will stay the same despite how many times it is forwarded. In this situation, there is high heritability. Of course, if heritability is perfect then there will be no variation; but if heritability is too flawed, then selection will have trouble producing anything cool because things will get too garbled too quickly.

It seems like the best idea is to have almost perfect copying, but allow for small mistakes to sometimes seep in, to provide for modest variation. This is what natural evolution does; each of us has tiny mutations in our DNA that make us unique.

Evolution, in nature, in a nutshell:
1) Selection – is natural selection, that creatures better at surviving will pass on their genes, meaning that in general the ability to survive tends to improve over time.
2) Variation – happens through animals having unique DNA, which occurs through infrequent errors when copying DNA and also through mating, which makes a mix of two existing DNAs from different parents.
3) Heritability – happens because copying errors are infrequent in DNA, so the game of telephone between parent’s DNA and child’s DNA is accurate. There may be some small changes, but if these changes are too severe — for example, a frog born with an additional leg, that frog is unlikely to survive to pass on its genes.

Evolution of Hip Hop

What is cool about evolution is that it is *general*, it isn’t just confined togenes and DNA. For example, ideas also evolve. Leeches are no longer best practice for treating disease and fanny-packs and pogs are no longer cool. Right now, paranormal romance (read twilight, etc.) is particularly popular, but twenty years from now, some other genre will be in vogue.

Music evolves too! A branch of blues music evolved into funk, and a branch of funk led to hip-hop. We tend to support those artists with addictive, cool-sounding new songs, and variations of those songs fill the air-waves. Musical ideas are ‘selected’ by listeners who buy albums or call into radio stations to request songs. These musical ideas vary over time: Artists inspired by a cool song will make new songs with similar sounds or traits, and other artists might be inspired by this new song. The evolution of cultural ideas like fads or music is called memetics, which is an intriguing topic in its own right.

However, right now, I want to discuss artificial evolution within a computer, which is but a hop, skip, and a jump away from finally understanding neuroevolution!

Evolving bits

When you were in middle school, your teacher gave you annoying algebra problems to solve. She’d say, “Hey, Joel, find the value of x for this equation: 2x-10=3.” Listen, lady, I’d sure love to but there’s a Buffy marathon on TV. Wouldn’t it be cool if we could let evolution solve this math problem for us while we eat ham sandwiches instead?

The answer, is yes, of course! We all love ham sandwiches and despise intellectual labor. The question, though, is how we can set up those three factors that cause evolution (selection, variation, and heredity) to do our homework for us?
Let’s start with heredity.

1) Computerized Heredity
In nature, DNA is what is changed by evolution. For evolution in a computer, we can make our own DNA up. Whatever we want. Muahahaha. It can be as simple as a list of numbers. For simplicity’s sake, it can even be just a single number.
Okay. So now we have our artificial DNA that is of just one number. Let’s call this one number x, because that is what we are trying to find to solve this lame algebra problem. So, our ideal piece of artificial DNA, which is just a number, will contain the correct value of x, the one that makes the equation true.

We can make copies of this artificial DNA, this one number, by simply writing down this number in a different place. These copies of that number are little chidldren DNAs of the original artififical DNA. Because these copies of the DNA resemble each other (well, they are the same), we’ve achieved heredity! Boom.

2) Computerized Variation
Okay, well, how can we make variations of this artificial DNA, this one number? How about when we copy a parent DNA number to a child DNA number, we make a slight random change to it. We just add a little bit or subtract a little bit. This way, the child number will resemble the parent number, but it won’t be exactly the same. So, the parent number might be 2.31, and the child might be 2.35 or 2.25. In this way, the children will vary. Boom.

3) Computerized Selection
The last element of this computerized evolution game is selection. We need to come up with a way of selecting those pieces of artificial DNA that are closer to solving our algebra problem than others.

One way of doing this is just plugging the artificial DNA x into the equation, and seeing how close it is to making the equation true. For example, if we set x to be 1 in our equation of 2x-10=3, we get 2-10=3 or -8=3. The left side is 11 different from the right side. We can say that we want to select those x’s that make the difference between the left side and right side of the equation smaller. If we set x to be 2, we get 4-10=3 or -6=3. In this case, the left side is 9 different from the right side, which is a smaller error than when x was 1. So, given a choice between artificial DNA with x=1 and x=2, we’d select x=2.
Our automatic selection mechanism plugs in the artificial DNA x into the equation and calculates how big the error is. We choose the DNAs that make this error the smallest.

It’s magic

We can now make a recipe for solving our little math problem. This is called an evolutionary algorithm, because it employs evolution in a methodical way that can be computerized.
Step 1: Put ten Artifical DNAs in a list (aka pick ten random numbers)
Step 2: Assign a score to each artificial DNA based on its error when we plug it into the equation 2x-10=3 (the higher the error, the worse the artificial DNA is). If the error is really small quit, otherwise go to step 3.
Step 3: Make a new list by taking the five best artificial DNAs from the last list and writing them down twice; when writing down a number, add or subtract a small number from it first to generate some variation.
Step 4: Go to step 2

Magic in practice

So I went ahead and translated our little recipe into Python, an actual computer language. You can look at the code here if you are curious. Each time through the loop described in steps 2 and 3, the program prints out the error of the best artificial dna and its x value. Next we’ll look at a print-out from a run, and then a graph. You can see that it quickly finds the solution to our equation 2x-10=3, which turns out is 6.5.

Loop # 1  Lowest error: 2.48  Best DNA: 5.26
Loop # 2  Lowest error: 2.35  Best DNA: 5.32
Loop # 3  Lowest error: 2.24  Best DNA: 5.38
Loop # 4  Lowest error: 2.15  Best DNA: 5.42
Loop # 5  Lowest error: 2.07  Best DNA: 5.46
Loop # 6  Lowest error: 2.03  Best DNA: 5.49
Loop # 7  Lowest error: 1.88  Best DNA: 5.56
Loop # 8  Lowest error: 1.79  Best DNA: 5.60
Loop # 9  Lowest error: 1.72  Best DNA: 5.64
Loop # 10  Lowest error: 1.68  Best DNA: 5.66
Loop # 11  Lowest error: 1.57  Best DNA: 5.72
Loop # 12  Lowest error: 1.43  Best DNA: 5.79
Loop # 13  Lowest error: 1.47  Best DNA: 5.77
Loop # 14  Lowest error: 1.30  Best DNA: 5.85
Loop # 15  Lowest error: 1.14  Best DNA: 5.93
Loop # 16  Lowest error: 1.04  Best DNA: 5.98
Loop # 17  Lowest error: 0.95  Best DNA: 6.03
Loop # 18  Lowest error: 0.76  Best DNA: 6.12
Loop # 19  Lowest error: 0.77  Best DNA: 6.11
Loop # 20  Lowest error: 0.72  Best DNA: 6.14
Loop # 21  Lowest error: 0.61  Best DNA: 6.20
Loop # 22  Lowest error: 0.49  Best DNA: 6.25
Loop # 23  Lowest error: 0.30  Best DNA: 6.35
Loop # 24  Lowest error: 0.44  Best DNA: 6.28
Loop # 25  Lowest error: 0.28  Best DNA: 6.36
Loop # 26  Lowest error: 0.25  Best DNA: 6.37
Loop # 27  Lowest error: 0.13  Best DNA: 6.43
Loop # 28  Lowest error: 0.01  Best DNA: 6.50

And here is a little graph showing how error decreases to around zero over time:

So what we’ve shown here is that it is possible to harness evolution to solve problems within a computer. We could have it solve other equations by changing the error function. One cool aspect of evolving solutions to problems is that we just specify what we are looking for, and evolution will try and find it.

While our artificial DNA here was just a single number, the artificial can be more complicated. For example, we could evolve x and y for a more complicated equation. But more interesting than this trivial addition is neuroevolution, where the artificial DNA does not represent a sequence of numbers but an artificial brain that can control robots. Through neuroevolution we can get robots to do cool things while we eat ham sandwiches.

Darwin meets Frankenstein

What’s in a brain, anyways? Basically our brain is a collection of neurons that are wired together in various ways, like an incredibly complicated circuit. Neurons are cells that do basic computation. They can get signals from the real world (like from our eyes or ears) or control our muscles. Neurons are what enable us to sense the world and do things. A bunch of neurons centralized in our brain is what give us instincts and thoughts.

Now, if we want to make an artificial brain for a robot, we can think of a brain as a collection of neurons and wires that connect them together. In the context of a robot, these wires may connect neurons to the robot’s motors or to its sensors (like a video camera), so that the robot can move in response to how it sees the world. The wires may also just connect neurons to each other.

Intermediate neurons that sit between the sensors and the motors can compute functions of sensory inputs to enable more sophisticated robot behaviors. For example, running away when you smell a predator is a simple behavior that can be accomplished by directly connecting the nose sensor to the motors. However, predicting the trajectory of a moving baseball might require doing some basic calculations that require lots of neurons connected in complicated ways.

But beyond understanding how a robot could have an artificial brain and what such a brain might be built from, what we would really like to do is to have evolution design these artificial brains for us, which is the essence of neuroevolution. A simple way to do this is to construct an artificial DNA that acts as a wiring diagram for an artificial brain. You can imagine that such diagrams could be twiddled slightly, by changing the strength of a connection between two neurons, or adding in new neurons, or by adding or removing connections entirely. This is how evolution can mutate an artificial robot brain.

And so you can implant these robot brains in a robot, turn the robot on, and see what its brain induces it to do. Different brains can cause different behaviors because they will enact differing policies. One brain’s policy might be to purposefully ram into walls, another might spin aimlessly in circles. The question remaining is how can we use evolution now to get a brain that does something we want?

Like we did in the case of evolving the solution to the equation, we need a measure of goodness. This measure can aide us to select good robot brains and to throw away the bad ones. Perhaps you want to evolve a robot that can navigate a corridor. One measure of goodness for evolving such a policy is to look at where the robot ends up, and see how far it is from where we would like it to be.  That is, imagine we always start a robot at the beginning of a corridor, and let it roam for awhile. After a fair amount of time has passed, we look at its position. If it is near the end of the corridor, we deem it as good.

With the ability to represent a brain as a wiring diagram, to slightly mutate these diagrams, and a way of evaluating how good these diagrams are, we are ready to craft our first neuroevolution experiment!

Magic part two: Evolving Robot Brains

We can now make a recipe for solving our corridor navigation problem with another evolutionary algorithm.
Step 1: Put one hundred Aritifical Brain DNAs in a list (aka make one hundred random wiring diagrams)
Step 2: Assign a score to each artificial DNA based on how far a robot gets through the corridor when we plug in the brain the artificial brain describes. The farther the robot is from the end of the corridor than the worse the artificial DNA is. If the robot gets very close to the end then we are successful and we can stop, otherwise go to step 3.
Step 3: Make a new list by taking the fifty best artificial DNAs from the last list and writing them down twice. Then slightly change the wiring diagrams of all of these DNAs to induce some new variation.
Step 4: Go to step 2

Frankenstein in the Corridor

I went ahead and codified this experiment as well, the source code is written in Python and is available through github. Here is a picture of the corridor:

This is a screenshot from the corridor simulator, viewing the corridor from a top-down perspective.  The blue X’s are the walls of the corridor, the grey + is the robot’s intended destination, and the red line is the robot. The green stars projecting from the robot are a visualization of its wall sensors, which are also visualized at the bottom of the screen.

After 200 generations, usually the evolutionary algorithm has evolved a brain that can navigate the corridor. Now, for the fun part, a few videos showing a few examples of evolved artificial brains. The first video is from an intermediate solution, one that does not completely make it through the corridor.



The next video is from a solution:



What is really cool here is that evolution has discovered a (albeit simple) brain that can drive a simulated robot through a corridor. We didn’t have to program it to accomplish the task, we trained it. Our measure of how close a robot got to the end of the corridor was used to guide evolution towards a good brain.

It isn’t always easy to train artificial brains (and in fact these difficulties are what my research is centered on), but I can remember how excited I was when I discovered that evolution could be used within a computer to automatically learn things. Hopefully I’ve propagated some of that excitement to you.

Email’s not sexy

I wanted to host an email server for a project I am working on. Due to the simplicity of installing a web server in modern linux distributions I mistakenly assumed I was a few “apt-get install”s away from success. This was stupid of me.

Don’t get me wrong, I am sure that sendmail and postfix are wonderful pieces of powerful software, and as someone searching for free software to do complex things I have no right to complain, but I simply don’t care enough about email to invest time in learning. It’s just not fun or sexy to me. For whatever reason, web servers are sexier. Web servers are still tied to the future and are going interesting places. But email seems bland and tired, no longer tied to progress, like some sort of dead end, waiting to be replaced by some cooler communication system.

Basically, my search for a simple solution led me here: https://help.ubuntu.com/community/MailServer , which tells me exactly what I don’t want to hear:

Setting up an email server is a difficult process involving a number of different programs, each of which needs to be properly configured. The best approach is to install and configure each individual component one by one, ensuring that each one works, and gradually build your mail server.

Great. Perhaps my technical genius will allow me to plow through this in a few minutes?

A Mail Transfer Agent (MTA) is the program which receives and sends out the email from your server, and is therefore the key part. The default MTA in Ubuntu is Postfix, but exim4 is also fully supported and in the main repository.

Postfix – this guide explains how to set up Postfix.

But the extent of my technical genius is vastly (well, entirely) overstated and my attention span is near it’s limit. I hope this is relatively simple.

[...]

Configure Postfix to do SMTP AUTH using SASL (saslauthd):

sudo postconf -e 'smtpd_sasl_local_domain ='
sudo postconf -e 'smtpd_sasl_auth_enable = yes'
sudo postconf -e 'smtpd_sasl_security_options = noanonymous'
sudo postconf -e 'broken_sasl_auth_clients = yes'
sudo postconf -e 'smtpd_recipient_restrictions = permit_sasl_authenticated,permit_mynetworks,reject_unauth_destination'
sudo postconf -e 'inet_interfaces = all'

Next edit /etc/postfix/sasl/smtpd.conf and add the following lines:

pwcheck_method: saslauthd
mech_list: plain login

Generate certificates to be used for TLS encryption and/or certificate Authentication:

touch smtpd.key
chmod 600 smtpd.key
openssl genrsa 1024 > smtpd.key
openssl req -new -key smtpd.key -x509 -days 3650 -out smtpd.crt # has prompts
openssl req -new -x509 -extensions v3_ca -keyout cakey.pem -out cacert.pem -days 3650 # has prompts
sudo mv smtpd.key /etc/ssl/private/
sudo mv smtpd.crt /etc/ssl/certs/
sudo mv cakey.pem /etc/ssl/private/
sudo mv cacert.pem /etc/ssl/certs/

Configure Postfix to do TLS encryption for both incoming and outgoing mail:

[...]

Oh my god I don’t care anymore. I don’t understand why this sensible configuration isn’t built in or automated, there probably are wonderful technical reasons, but I am physically unable to force myself to type in these commands because I am bored just reading them.

If this was Node.js or clojure, the compelling nature of what they enable and how they sit at the edge of innovation might entice me to dig through config files — and yet ironically I don’t need to because the default install for those programs are fairly straightforward.

Anyways, moral of the story: The amount of garbage you are willing to put up with to get something working reflects how inherently interesting you deem that endeavor. Keep that in mind the next time you feel your temperature rising when dealing with config files. Perhaps some things are worth outsourcing instead of buckling down and working through. I feel like an intermediate knowledge of web servers will be handy in future projects, whereas becoming intimate with IMAP, SASL, MTA, and MX DNS records probably does not pave a path towards the next big thing.

Bookalyzer: Exploiting Critical Mass to Make Magic and Explore History

One reason I love linux is the wide array of packages that can either be instantly installed from the command line or easily downloaded from third party sites. While this doesn’t necessarily distinguish linux from windows, the linux ecosystem is designed for power users.  With Linux you can quickly cobble together an impressive tool from wide-ranging components using a scripting language as glue.

Because the system of components available for linux has reached a critical mass (just about anything you might need probably exists), the things you can accomplish in four hours of tinkering are surprising. For example, in this post I detail a tool I made that can investigate whether our literature is getting dumber.

The Problem: Monotonous Word Counting

For a research project I was looking to estimate word counts of popular books and their readibility (i.e. is a particular book written for a highly educated audience or the masses?). One characteristic of hackers is that they are lazy in a special sense: they generally dislike drudging intellectually-void work like manually counting words on a page. So, I investigated automated alternatives.

Bookalyzer: Scraping Google Books Previews

I noticed that excerpts from many books are available through google books. However, the text is not copy/paste-able (i.e. it is an image rendered through javascript). In order to automatically analyze a book’s contents I would need to convert the images into machine-friendly text, not a simple task.

Whimsically and unrealistically, I thought it’d be great to have a tool that would: 1) control a web-browser to use google books, 2) go to an arbitrary page,  3) take a screenshot, 4) run the screenshot through OCR (optical character recognition) and 5) analyze the resultant text. It seems like an ambitious ungainly project, especially since I hadn’t had any experience with browser automation or OCR tools.

Naturally, my initial rational impulse was to give up and just do the work manually. Luckily though, my allergy to dull work prevailed. In fifteen minutes of web searching, a somewhat realistic plan had congealed:

1. From the title of the book, query the google books api to determine an ISBN

2. Feed the ISBN into a html document that uses the google books embedded viewer api to zoom in and scroll a few pages in to reach a representative page (hopefully full of text).

3. Use selenium to drive firefox to render the html document and take a screenshot

4. Take the screenshot, do some cropping and basic segmentation with imagemagick to isolate the text

5. Translate the image into text through tesseract, an open-source OCR engine that is fairly good.

6. Finally, use the page count and the words on this particular page as a (admittedly rough) estimate of the book’s word count, and calculate a basic readibility metric

Surprisingly, this plan worked; I was able to implement a basic functional version of the tool in about four hours. I’ve posted my code on git-hub if you would like to leapfrog from it, although it is a hack. I’m calling it bookalyzer.

Dummy Test: Does It Measure Anything

The text gets a bit garbled from the OCR; it isn’t perfect. Also, sometimes the page you choose from the google books sample might not be representative of the whole book (e.g. perhaps you choose a particularly dense page). Both of these points imply that there will be some noise in the readibility measure.

So, to test whether bookalyzer measures anything at all, I ran the tool on a set of biology textbooks and on children’s fiction (a selection of R.L. Stein’s Goosebumps series, for those that remember). The question was whether the bookalyzer tool could differentiate the reading levels of these two sets. Here is a plot of the resultant readibility scores:

You can see that there is a clear difference: The children’s books have an average readibility of around 5th grade, while the Biology textbooks float around an 11-12th grade reading level. So, despite the noise, the readibility test run on an OCR’d page of a google-book preview has some measuring power.

Fun Application: Are Books Getting Dumber?

It seems somewhat believable that best-selling books might be getting dumber over time. We think of past generations as possibly more well-read, and of the current generation (perhaps unfairly) as celebrity-gossip-seeking Jersey-shore-watching idiots. Perhaps every generation believes the next is stupider.

Interestingly, given the ability to estimate the readability of any google-previewable book and a list of best-selling books over a few decades, one can actually investigate this claim (albeit on a superficial level). I grabbed a list of bestselling books going back a few decades from a class website and ran the readibility tool. Here are the results:

The data does suggest a slight downwards trend (-0.03 grades per year),  although the correlation was weak (-0.09) and the p-test was not significant (0.18). In other words, we might be getting dumber, but the data is not conclusive.

Someone could probably do a better job either (and probably someone already has) if they 1) work at google and have full access to the text of all these books, or 2) using the ngram dataset dataset from google (http://ngrams.googlelabs.com/datasets) in a clever way with a word-based readibility metric.

Conclusion

Powerful open platforms like Linux and freely-available internet APIs (like google books) organize into a critical mass that potentiates a limitless swathe of unforeseen applications. What strange magic can you bring to life in four hours?

Ubuntu/Linux: What to do when a window or dialog won’t fit on-screen

On my laptop, sometimes an application’s throws up a pop-up menu or form that is too long to fit on the screen. If the form has no scroll-bar to get to the bottom of the form, which often has an OK button that needs to be pressed to move on, it is a very frustrating experience.

I’ve had this problem with cinelerra, a powerful opensource video editor  as well as with the android SDK. The solution is to press ALT+F7, which will allow you to ‘grab’ the window and manually adjust it upwards and allow you to click the OK button and move on!

Human Oven Simulators and Theoretical Computer Science

“I like cinnamon, so I’ll season the soup with that. Well, the flavor of basil is nice too, so in that goes. And pesto! And chocolate chips! And chicken fingers! And motor oil!”

Cooking disasters

Those just learning how to cook often become overeager and combine too many conflicting ingredients. The inevitable result is an abomination of nature necessitating a thoroughly trained team of serious men in haz-mat suits who say grizzled things like “Holy mother of God,” in dramatic drawn-out timbre. The problem us novice cooks face is that how good something tastes is not a simple combination of how good the individual ingredients taste.

Cooking is surprisingly deep.  Nearly always, an outsider’s view of a particular subject is off-base. For example, people not familiar with the wild world of computer science generally assume that it is all about fixing computers, when in fact it all about hard drugs and loose women — fine, ok, not that either. Surprisingly, computer scientists are not always experts at figuring out why ITunes won’t load or deciphering arcane error codes in Microsoft Excel. Instead, computer scientists are universally adept at translating human thought and language into an algorithm that a computer can “understand” and run. Us computer scientists take a process (for example, sorting a list of numbers) and turn it into a recipe so unambiguous and literal that a dumb-as-rocks CPU can follow the instructions. Outsiders don’t generally know this, though. Silly geese.

I was mistaken about cooking in a similar way. My outsider’s view of cooking was that it was fundamentally about following directions. You take a recipe, and the more accurately you follow that recipe, the better you are at cooking. But this is a superficial view of cooking; to a certain point your technical ability to follow recipes is important. However, the undeniable rock star with only a tenuous grasp of English, traditional musical knowledge, and basic instrumental skills illustrates that technique is not everything. And for all those cooks that do master the technical skills, what then distinguishes a brilliant chef?

A deeper view might focus not only on technical skill, but also on the talents required to bring delicious new recipes into reality. The challenge in making good recipes is that on some level you need to understand how different ingredients and cooking methods will interact to produce a taste. That is, to tweak an existing recipe so that it tastes better, you might identify some deficiency in the flavor and then figure out how to remedy that problem.

This is sometimes easy — if the food is too sour, adding a sweetener like sugar will generally help. However, improving a complex mix of spices requires understanding how those spices interact together, what is missing from the interaction, and how adding or removing a quantity of another spice can remedy the flaw. In other words, becoming a master chef requires building a detailed mental model that maps recipes to how they will taste.

You must become a human oven simulator.

Besides the tasty products it leads to, cooking can also provide an intuitive metaphor that can illustrate complex issues in computer science or mathematics. For example, say you have a spicerack and want to make a mix of spices (say, to season a soup) that tastes better than some existing mix (suck it, Lowry’s seasoning salt). Surprisingly,this is actually a very hard problem because spices interact in complicated ways. The effect of a spice on your tastebud — whether it will improve the flavor or not –depends on the context of that spice, i.e. what spices it is mixed with. For example, chilli powder may taste good when mixed with paprika and black pepper, but less so with vanilla extract. So, making a better spice mix problem is surprisingly hard. So hard that it is an NP-complete optaimization problem in disguise.

NP completeness: Scary-sounding yet simple

Don’t be afraid. Here comes the segue into theoretical computer science. I promise that I’ll keep things understandable. First, take the triple integral of the hyperbolic tangent of x, and then obviously we will apply the Weissman transformation, because only a complete idiot wouldn’t! Just kidding.

Although at first you might reasonably think that it has absolutely no relation to real life, theoretical computer science deals with an abstraction of real-life processes called algorithms. This is similar to how the ‘x’ in ‘x+3=5′ in algebra is an abstraction of a number. So just as ‘x’ could represent any real-life quantity — in this equation it could readily represent the number of warm tequila shots needed to induce vomiting — an algorithm in computer science can represent any real-life process, like the steps in a recipe one follows when cooking.

Now, before this digression I had mentioned that trying to improve a mix of complex spices is equivalent to an NP-complete optimization problem in theoretical computer science. ‘Optimization’ is just a fancy word for ‘trying to improve’, but what is ‘NP-complete’?

NP-complete means that a problem is very difficult to solve, and yet a correct answer is easy to verify (for example, it is difficult to get a girl’s number at a club when you are dressed up like a giant banana, but you’d know you were successful by dialing the number on a piece of napkin and hearing her voice). For our spice example, simply by tasting both the better spice mix and the benchmark Lowry’s seasoning salt (sponsor me?), you can easily verify if the problem has been solved or not: Does the new mix taste better? However, to come up with this better spice mix may take a lot of work.

In fact, one of the biggest open problems in theoretical computer science is whether you can find some way to easily solve  NP-complete problems, or whether they can only be solved by doing an outrageous amount of brute-force work (e.g., trying every conceivable combination of spices). This is known as ‘P=NP?’. P is the set of easily-solved problems, and NP is the set of easily-verified problems. Most people think these two sets are not the same, that some easily-verified problems (for example, our spice rack optimization problem) cannot be easily solved. But as of yet no one has been able to prove it, though many geniuses have tried.

Reverse-engineering Coke’s secret formula or a rocking chair

There’s an interesting analogy between the idea of recipes in cooking and that of a computer program in computer science. Both recipes and programs describe processes, but a recipe is interpreted by a human and a computer program by a computer. With this rough analogy in mind, I’ll ask a seemingly unrelated question: Is it possible to reverse-engineer any recipe? That is, by looking at the cooked food, can we uncover a potential list of ingredients and how they are to be combined and cooked, that generates something that tastes the same? Perhaps a good enough chef, given enough time and smarts could deduce the recipe for any food.

But maybe this underestimates the trickiness of the problem. While chefs are well-acquainted with foods that taste good or that are made in typical ways, what about recipes that are random combinations of different ingredients and cooking methods (grilled cheerio-tuna paste with creamed-celery and vinegar marinade)? They might generate gross, weird foods that a chef would have no experience in dealing with. These strange creations would lie outside the chef’s mental model of food-tastes and might be more difficult to reverse-engineer into a recipe.

The difficulty of reverse-engineering a complex artifact (like a cooked food) is not specific to cooking. For example, take the art of wood-working. When doing wood-working, one applies tools (saws, drills, chisels) in a systematic way to achieve a certain appearance in the wood. That is, there are certain techniques that are performed on the wood in a certain order, like steps in a recipe, to transform the wood in a particular way. So, given a final assembled piece of worked wood, is it always possible to determine a reasonably short list of  actions similar to those that were actually taken? With simple pieces, it is probably easy to determine how to achieve a particular look. However, with a large set of complex cuts and chisels, trying to deduce the “recipe” to create that finished piece may be very difficult.

Woodworking with 1′s and 0′s

While these strange reverse-engineering situations might seem pointless, they relate to the grand issue of “P=NP?” in computer science (can difficult problems that have easily verified solutions be solved easily?). Computer programs can be seen as abstract versions of recipes or wood-working plans. But instead of  a cooked food or a finished piece of wood, a computer program crafts abstract data, a series of bits, 1′s and 0′s. Computer programs consist of instructions, much like recipes, that run for awhile and do various calculations on data.  For example: “Take the number 27, multiply it by 3, keep dividing it by two until the remainder is 0, then print out how many times we divided.” We can consider a type of program that prints out a single number on the display when they finish. We can view this lonely number as the product, what the algorithm creates, and abstract equivalent of food in recipes, or the final piece when woodworking.

So, we can ask a reverse-engineering question about computer programs similar to the ones we asked earlier about cooked food or finished pieces of wood. Can we examine any given very long number (say tens of thousands of digits) and then determine a small program, if one exists, that produces it? It is important that the program be small, because a simple way of generating any number is just to say “Print x” where x is that big number. This isn’t very interesting, it would be similar to if the recipe for a particular cake was an atom-by-atom description of the cake, or if the instructions for creating a table for woodworking detailed how to glue together a huge amount of tiny wood pieces.

For example, if the binary number (series of 1s and 0s) was “111111111111111111111111111″ a simple, quick algorithm for making this string is just “Print 1 thirty times.” This is a good recipe for making that string of bits. For a random string of bits, like “101101001011110010101111″ there may be no short recipe for constructing it. Can you think of one?

We also might want to say that a number-recipe program shouldn’t run forever. That is, some programs might specify really long calculations that could take eternity for a real computer to run. Like: “Consider all of the numbers less than 20 trillion, factor them, and add all of their factors together.” A time restriction makes sense because we also wouldn’t want a recipe for cheesecake that requires 33.5 degree heat applied for a millennium. So perhaps we add some arbitrary cutoff, say, that a number-recipe program can only run for a number of steps that is proportional to the size of the target number, the one to be printed out. If the cooked number is 1000 digits long, perhaps the program can only run for 1000 squared, or 1,000,000 steps. With these constraints considered, what we are asking then is if given a really long number, we can come up with a relatively short, fast recipe for generating that number.

For example, imagine our problem is to find a small, fast recipe for the number “10110111011110111110 …” (what is the pattern here?) that continued until there were a thousand ones followed by a last zero. A potential recipe is “Do the following one thousand times: Print ’1′ however many times we’ve done this step and then print a single ’0′.”

Look at me, now back at NP…I’m on a horse

Now to tie this sprawling post together: How does this number-recipe-writing problem relate to “P=NP?” Remember that this grand unsolved problem in computer science asks if every problem in which solutions are easily verified (NP) is also easily solved (P). Our reverse-engineering problem is easily verified (it is in NP): If you take a short program and run it, you can discover if it stops running within the time limit and if the number it outputs at the end is the one we are interested in. What is not clear is if it is also in P, that is, whether NP problems are easily solvable.

Intuitively, it seems like this problem shouldn’t be easily solvable, that it should not be in P. The space of possible programs is so vast, and the mapping between programs and output numbers so strange, that there should be no automatic way of reverse-engineering a given number to deduce its origins . This is why I, and most computer scientists, believe that P is not equal to NP, though it is still an unsolved problem.

So, as we reach the end of this long strange thread, the take home message is that although it seems far removed from reality, theoretical computer science actually does have something to say about what is easily possible in reality. That is, it may be impossible to easily reverse-engineer an arbitrary process, whether it is a computer program, a recipe, or instructions to craft wood. Another take-home message is that to avoid creating kitchen monstrosities, when first learning to cook it is good to stick to the recipes instead of boldly going where no man has, nor ever should go, into that wild and pungent frontier of culinary catastrophes.